Multiplicación de polinomios

Multiplicación de polinomios

El siguiente ejemplo es el producto de un monomio por un binomio:

Este mismo principio —multiplicar cada término del primer polinomio por cada uno del segundo— se puede ampliar directamente a polinomios con cualquier número de términos. Por ejemplo, el producto de un binomio y un trinomio se hace de la siguiente manera:

Una vez hechas estas operaciones, todos los términos de un mismo grado se han de agrupar, siempre que sea posible, para simplificar la expresión:

Factorización de polinomios

Dada una expresión algebraica complicada, resulta útil, por lo general, el descomponerla en un producto de varios términos más sencillos. Por ejemplo, 2x3 + 8x2y se puede factorizar, o reescribir, como 2x2(x + 4y). El encontrar los factores de un determinado polinomio puede ser materia de simple inspección o se puede necesitar el uso de tanteos sucesivos. Ciertos polinomios, sin embargo, no se pueden factorizar utilizando coeficientes reales y son llamados polinomios primos.

Algunas factorizaciones conocidas aparecen en los ejemplos siguientes.

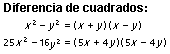
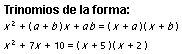
Para factorizar suele ser útil agrupar primero; aquellos términos que sean similares se agrupan como en el siguiente ejemplo, cuando sea posible:

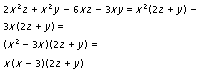
Máximo común divisor

Dado un polinomio, suele ser importante determinar el mayor factor común a todos los términos del polinomio. Por ejemplo, en la expresión 9x3 + 18x2, el número 9 es un factor de ambos términos, lo mismo que x2. Tras su factorización se obtiene 9x2(x + 2), y 9x2 es el máximo común divisor de todos los términos del polinomio original (en este caso un binomio). De la misma manera, en el trinomio 6a2x3 + 9abx + 15cx2, el número 3 es el mayor submúltiplo común a 6, 9 y 15, y x es el mayor factor de la variable común a los tres términos. Por tanto, el máximo común divisor del trinomio es 3x.

Mínimo común múltiplo

Encontrar el mínimo común múltiplo es útil para poder hacer ciertas operaciones con fracciones algebraicas. El procedimiento es similar al usado para realizar estas operaciones con fracciones ordinarias en aritmética. Para poder combinar dos o más fracciones, los denominadores deben ser iguales; la forma más directa de obtener un denominador común es multiplicar todos los denominadores entre sí. Por ejemplo:

Pero puede ocurrir que bd no sea el mínimo común denominador. Por ejemplo:

Sin embargo, 18 es sólo uno de los posibles denominadores comunes; el mínimo común denominador es 6:

En álgebra, el problema de encontrar el mínimo común múltiplo es similar. Dadas varias expresiones, su mínimo común múltiplo es aquella expresión con el menor grado y los menores coeficientes que se puede dividir exactamente por cada una de ellas. Así, para encontrar un múltiplo común a los términos 2x2y, 30x2y2, 9ay3, basta con multiplicar las tres expresiones entre sí y es fácil demostrar que (2x2y)(30x2y2)(9ay3) se puede dividir exactamente por cada uno de los tres términos; sin embargo, éste no es el menor de los múltiplos comunes. Para determinar cuál es el mínimo, cada uno de los términos se ha de descomponer en sus factores primos. Para los coeficientes numéricos, 2, 30 y 9, los factores primos son 2, 2·3·5 y 3·3 respectivamente; el mínimo común múltiplo de los coeficientes debe ser por tanto 2·3·3·5, o 90, que es el producto de la mínima cantidad de factores necesaria para obtener un múltiplo común. De la misma manera, como la constante a sólo aparece una vez, debe ser un factor. En cuanto a las variables, se necesitan x2 e y3; por tanto, el mínimo común múltiplo de los tres términos es 90ax2y3. Esta expresión se puede dividir exactamente por cada uno de los términos.

Resolución de ecuaciones

Dada una ecuación, el álgebra se ocupa de encontrar sus soluciones siguiendo el concepto general de identidad a = a. Siempre que se apliquen las mismas operaciones aritméticas o algebraicas en ambos lados de la ecuación la igualdad se mantiene inalterada. La estrategia básica es despejar la incógnita en un lado de la igualdad y la solución será el otro lado. Por ejemplo, para resolver la siguiente ecuación lineal con una incógnita

los términos que contienen la variable se despejan en un lado y las constantes en el otro. El término 3x se puede eliminar del lado derecho mediante sustracción; 3x se ha de restar del lado izquierdo al mismo tiempo:

Después se resta el número 6 de ambos lados:

Para despejar la x en el lado izquierdo se dividen ambos lados de la ecuación por 2:

y la solución es por tanto: x = 3. Para comprobar este resultado basta con sustituir el valor x = 3 en la ecuación original:

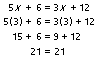
Resolución de ecuaciones cuadráticas

Dada una ecuación de segundo grado o cuadrática en su forma general:

hay diversas posibilidades para resolverla dependiendo de la naturaleza específica de la ecuación en cuestión. Si la ecuación se puede factorizar, la solución es inmediata. Por ejemplo:

Primero se escribe la ecuación en su forma general

que se puede factorizar como:

La igualdad sólo se cumple cuando uno de los factores es cero, es decir, cuando x = 5 o x = -2. Éstas son las soluciones de la ecuación, que de nuevo se pueden verificar mediante sustitución.

Si a primera vista no se encuentra un modo directo de factorizar la ecuación, puede existir otra alternativa. Por ejemplo, en la ecuación

la expresión 4x2 + 12x se podría factorizar como un cuadrado perfecto si fuera 4x2 + 12x + 9, que equivale a (2x + 3)2. Esto se puede conseguir fácilmente sumando 9 al lado izquierdo de la ecuación. La misma cantidad debe sumarse, por supuesto, al lado derecho:

que se reduce a

o

y

pues º tiene dos valores. La primera ecuación da la solución x = 1 (restando 3 de ambos lados: 2x = 1, y dividiendo ambos lados por 2: x = 1). La segunda ecuación da x = -7/2. Ambas soluciones se pueden verificar como antes, sustituyendo los valores en cuestión en la ecuación original. Esta forma de resolución se suele denominar método del cuadrado perfecto.

En general, cualquier ecuación cuadrática de la forma

se puede resolver utilizando la fórmula cuadrática. Para cualquier ecuación de este tipo las dos soluciones de x están dadas por la fórmula:

Por ejemplo, para encontrar las raíces de

primero se pone la ecuación en su forma general:

Por tanto, a = 1, b = -4 y c = 3. Estos valores se sustituyen en la fórmula cuadrática:

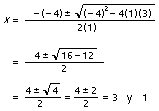
Sistemas de ecuaciones

En álgebra, lo normal es que haya que resolver no una sino varias ecuaciones al mismo tiempo. El problema es encontrar el conjunto de todas las soluciones que cumplen todas las ecuaciones simultáneamente. El conjunto de ecuaciones que deben resolverse se denomina sistema de ecuaciones y para resolverlo se pueden usar técnicas específicas del álgebra. Por ejemplo, dadas las dos ecuaciones lineales con dos incógnitas

hay un sistema sencillo: la variable y se despeja en la ecuación (2) dando y = 5 - 2x; este valor de y se sustituye en la ecuación (1):

Así el problema se reduce a una ecuación lineal con una sola incógnita x, obteniéndose

o

de donde

Si este valor se sustituye en cualquiera de las ecuaciones originales (1) o (2), se obtiene que

Otro método más rápido para resolver un sistema de ecuaciones es, en este caso, multiplicar ambos lados de la ecuación (2) por 4, con lo que queda:

Si ahora se resta la ecuación (1) de la (2), entonces 5x = 10, o x = 2. Este procedimiento genera otro avance en las matemáticas, las matrices. La teoría de matrices nos ayuda a obtener soluciones para cualquier conjunto de ecuaciones lineales con cualquier número de incógnitas.